Esercitazioni Matlab
II Parte AA2009/2010
es 1.
Considerare la sequenza ottenuta campionando la funzione s1(t)=exp(j*2*pi*t/T0) con T0=1 s, e dt=0.01. Fare il grafico sul piano di Gauss, parte reale-parte immaginaria della sequenza.
Evidenziare con due circoletti di diverso colore i punti s(0) e s(dt).
Fare i grafici rispetto al tempo della parte reale e della parte immaginaria di s1(t).
Ripetere le operazioni precedenti per s-1(t)=exp(-j*2*pi*t/T0).
Fare il grafico rispetto al tempo del segnale s(t)=s-1(t)+s1(t)
es 2.
Considerati i coefficienti complessi S1=5ej*pi/4 e S-1=5e-j*pi/4 si ripetano i punti descritti nell'esercizio 1, per i segnali s1(t)=S1exp(j*2*pi*t/T0), s-1(t)=S-1exp(-j*2*pi*t/T0) e s(t)=s-1(t)+s1(t).
es 3.
Dato lo sviluppo in serie di Fourier di un'onda quadra con periodo T0=2, dt=0.01 e T osservazione= 10 s
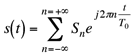
caratterizzato dai seguenti valori dei coefficienti. S0=0.5 e Sn=0.5*(sin(n*pi/2)/(n*pi/2)) per n0.
Fare il grafico rispetto al tempo delle componenti s|n|(t)=s-n(t)+s+n(t) per n=0, 1,2,...,9.
In pratica si avranno 9 grafici dove saranno visualizzate le componenti per n=0, n=1, n=2 etc. (N.B. in realtˆ i coefficienti per n pari sono nulli quindi la somma riguarderˆ solo n=0,1,3,5,7,9).
Sovrapporre a tali grafici il
grafico della onda quadra ottenuta tramite il comando square(.) di
matlab. es. onda_q=0.5+0.5*square(2*pi*(1/T0)*t+pi/2)
Considerare poi i segnali ottenuti in modo incrementale le varie componenti:
primo passo -> grafico di s0(t)+s|1|(t), secondo
passo ->grafico di s0(t)+s|1|(t)+s|2|(t)
etc.
Per valutare il contributo delle componenti a frequenza maggiore fare il
grafico della somma delle componenti dalla 5 alla 9, s|5|(t)+s|7|(t)+s|9|(t)
In ogni grafico confrontare con l'onda quadra completa.
es 4.
Date la sequenza periodica ottenuta campionando con tempo di campionamento T=1 s, il segnale tempo continuo x1(t)=cos(2*p*t/16), utilizzare l'algoritmo di fft per calcolarne la TDF. Tracciare i grafici modulo e fase della TDF. Curare la determinazione del corretto periodo delle sequenze campionate e la corretta taratura dell'asse frequenziale.
Fare il grafico sia dopo aver utilizzato fftshift, quindi centrando le frequenze attorno allo 0, sia senza utilizzare tale comando.
Utilizzare il comando ifft per stimare la trasformata discreta di Fourier inversa e farne il grafico confrontando il risultato con la sequenza di partenza.
es 5.
Calcolare la TDF del treno di impulsi dato dalla ripetizione periodica della sequenza
x[n]=[1 1 1 1 0 0 0 0 ].
Tracciare i grafici modulo e fase della TDF. Curare la corretta taratura dell'asse frequenziale. Fare il grafico sia dopo aver utilizzato fftshift, quindi centrando le frequenze attorno allo 0, sia senza utilizzare tale comando.
Utilizzare il comando ifft per stimare la trasformata discreta di Fourier inversa e farne il grafico confrontando il risultato con la sequenza di partenza.
es 6.
Realizzare l'operazione di convoluzione discreta nel dominio del tempo utilizzando il comando conv(.).
Come sequenze utilizzare x1=[1 1 1 1 1 1 1 1 1 1 ] e x2=[1 2 3 4 5 6 7 8 9 10].
Realizzare la convoluzione circolare tramite TDF. Porre
attenzione allo utilizzo dello zero padding.
Mostrare sia il risultato ottenuto senza lo zero padding e con lo zero padding
opportuno.
es 7.
Analisi spettrale tramite TDF.
Caso della sequenza finita x[n]=u[n]-u[n-5]. Calcolarne la trasformata di Fourier tramite la TDF.
Mostrare lÕeffetto dello zero padding con N=5, 10 e 20. Confrontare con la trasformata di Fourier calcolata analiticamente.
Vedere dispensa
es 8.
Si consideri la sequenza ottenuta campionando con T=1 s, il segnale x(t)=cos(2*p*t/8). Stimare la Trasformata di Fourier della sequenza ottenuta osservando il segnale per T_oss=8 s, 16 s, 100 s. Fare il grafico modulo e fase delle trasformate. Curare la taratura dell'asse frequenziale in ogni caso.
Ripetere la stima della trasformata utilizzando uno zero padding tale da avere N=100 campioni. Osservare la differenza tra aumentare la risoluzione operando lo zero padding, quindi aggiungere zeri, e aggiungere campioni, quindi aumentare il tempo di osservazione: in particolare osservare l'effetto del troncamento temporale del segnale sulla "vera risoluzione" frequenziale.
Vedere dispensa
es 9.
Fare il grafico modulo e fase della trasformata di Fourier del seguente sistema (fc=2Hz)
Per i valori dei poli e zeri di seguito indicati.
Per ogni punto riportare inoltre la posizione dei poli e degli zeri sul piano di Gauss (zeri con simbolo 'o', poli con simbolo 'x')
![]()
I) z1=0.8 z2=-0.9 zp1=0.8ejp/4 zp2=0.8e-jp/4
II)
z1=0.8
z2=-0.9 zp1=0.95ejp/4 zp2=0.95e-jp/4
III) z1=0.8 z2=-0.9 zp1=0.95ejp/2 zp2=0.95e-jp/2
Per alcune delle esercitazioni la dispensa LTI_Matlab.pdf
es 10.
Dato il filtro descritto dalla seguente funzione in z
![]() con a=0.5
con a=0.5
1) fare il grafico dei poli e degli zeri del filtro sul piano di Gauss
2) Calcolare la risposta in frequenza del filtro e farne il grafico del modulo e della fase
a. Realizzare
questa operazione sia stimando H(z) sulla circonferenza di raggio unitario,
ponendo ![]() con
con ![]()
b. Sia
utilizzando il comando freqz(B,A,w) dove B e A sono i coefficienti dei polinomi
in ![]() del numeratore e
del denominatore rispettivamente
del numeratore e
del denominatore rispettivamente
3) utilizzare la rappresentazione del filtro tramite coefficienti B e A per filtrare unÕonda quadra in ingresso. Utilizzare il comando filter(). L'onda quadra ha i seguenti parametri: Toss=100 s, T0=10s, dt=0.5s e deve variare tra 0 e 1
4) fare il grafico modulo e fase delle trasformate dell'ingresso e dell'uscita del filtro. Confrontare con i grafici dell'andamento temporale corrispondente e con la risposta in frequenza del filtro
5) stimare la risposta impulsiva h[n] del filtro mandando in ingresso una delta. La risposta impulsiva verra' in questo modo troncata visto che e' calcolata per un numero di punti uguale alla lunghezza della delta
La delta potra' essere del tipo delta=[1 0 0 ... 0]
Fare il grafico di h[n] ottenuta con delta di lunghezza 5 e successivamente di lunghezza 15
Confrontare la trasformata di Fourier di h[n] cosi' determinata con la risposta in frequenza teorica calcolata in 2.
6) Ripetere per a=0.95
es 11.
Ripetere i punti dell'esercizio 10 per i seguenti filtri
![]()
![]()
es 12.
Usare la dispensa Fir_finestre_ver_1_1.pdf come riferimento.
Calcolare la risposta impulsiva del filtro causale con M=10 e fL=2Hz.
Farne il grafico. Porre attenzione al caso n=M e al fatto che devo effettuare un rapporto tra vettori.
Calcolare la risposta in frequenza e farne il grafico curando la corretta taratura dell'asse frequenziale (freq. Campionamento= 20Hz)
Calcolare i valori delle finestre indicate nella dispensa. Farne il grafico nel tempo e in frequenza.
Applicare le finestre al filtro. Rappresentare il filtro ottenuto nel tempo e in frequenza.
es 13.
Applicare i diversi filtri dell'es 12 (in tutto sono 5) ad un'onda rettangolare con periodo T0=2s, d=0.5 valore medio 0.5 e valore massimo pari a 1.
Rappresentare ingresso e uscita nel tempo sovrapposti sullo stesso grafico.
Rappresentare trasformate ingresso e uscita.
Solo per un filtro a scelta eseguire l'operazione di filtraggio in tre modi diversi
1) tramite la convoluzione lineare (comando conv())
2) tramite la convoluzione circolare (attraverso la fft)
3) con il comando filter()
N.B. il filtro causale ha questa forma ![]() per
n=0..2M
per
n=0..2M
es 13.
Generare un vettore di 1000 numeri estratti da una ddp di tipo uniforme (comando rand()).
Utilizzare il comando histc per trovare l'istogramma dei
dati contenuti nel vettore. Fare in modo che gli intervalli dell'istogramma
siano tali da rappresentare tutti i possibili valori assumibili dagli elementi
del vettore: dividere l'intervallo tra il minimo e il massimo dei dati in un
numero di classi pari al primo intero maggiore uguale a ![]() .
.
Fare il grafico dell'istogramma utilizzando il comando stem (pi indicato per una distribuzione di una variabile a valori discreti) o il comando bar. Posizionare le barre al centro di ogni intervallo.
Normalizzare l'istogramma rispetto al numero di campioni (l'altezza di ogni barra approssima la probabilitˆ che la variabile assuma i valori del particolare intervallo). Farne il grafico.
Applicare all'istogramma ottenuto dall'operazione precedente una ulteriore normalizzazione rispetto alla larghezza degli intervalli (l'altezza di ogni barra approssima la densitˆ di probabilitˆ della variabile nel particolare intervallo). Farne il grafico.
es 14.
Generare un vettore di n numeri casuali estratti da un ddp gaussiana con valore medio pari a mu=10 e deviazione standard sigma=4. Utilizzare il comando randn() o normrnd(). Considerare il caso di numero di campioni n pari a 20 e 1000.
Farne l'istogramma nei due casi come nell'esercizio 13.
In ogni passaggio confrontare gli istogrammi con la distribuzione gaussiana con valore medio e deviazione standard uguale a quella, teorica, dei dati in oggetto. Ottenuto con il comando normpdf() e calcolata nei centri degli intervalli.
es 15.
Esercitazione Teorema Limite Centrale. Simulare il campionamento di m valori da n variabili aleatorie. Le variabili siano uniformemente distribuite tra 0 e 1. Riportare l'istogramma delle singole variabili. Considerare le n-1 variabili aleatorie costituite rispettivamente dalla somma delle prime due, delle prime tre, etc. variabili aleatorie originarie. Per ognuna di esse farne l'istogramma e confrontarlo con gli istogrammi delle singole variabili e delle altre variabili ottenute dalle somme.
es 16.
Ripetere l'esercitazione precedente dove le singole variabili aleatorie differiscono per varianza e valore medio.
N.B. per le successive esercitazioni potrebbe essere utile consultare la seguente dispensa (clicca qui)
es 17.
Generare due variabili indipendenti a distribuzione gaussiana.
Disegnare lo scatter plot, stimare i valori medi, le deviazioni standard, il momento congiunto del secondo ordine, la covarianza e il coefficiente di correlazione, nei seguenti casi
- le due distribuzioni hanno stessa varianza e valore medio;
- le due distribuzioni hanno stesso valore medio e varianze differenti;
- le due distribuzioni hanno stessa varianza e diversi valori medi;
es 18.
Generare due variabili a distribuzione gaussiana, linearmente dipendenti.
Utilizzare questo modello per la generazione y=a+b*x+eps, dove x una variabile distribuita normalmente con valore medio pari a 3 e deviazione standard pari a 2. eps distribuita normalmente con valore medio nullo e deviazione standard sigma=5. Potete scegliere a e b a piacere ad esempio 10 e 4 rispettivamente.
Disegnare lo scatter plot, stimare i valori medi, le deviazioni standard, stimare il momento congiunto del secondo ordine, la covarianza e il coefficiente di correlazione.
Ripetere le operazioni al punto precedente variando la deviazione standard di eps, sigma=1.
Ripetere nuovamente le operazioni variando il parametro b del modello.
es 19.
Generare due variabili a distribuzione gaussiana, linearmente dipendenti. Si possono usare i dati generati nella es 18).
Stimare i parametri di un modello di regressione lineare applicato alle variabili y e x.Disegnare lo scatter plot dei dati e sovrapporre la retta di regressione.
Calcolare l'errore del modello di regressione e farne l'istogramma.
Verificare il legame (che troverete nella dispensa indicata in precedenza) tra il valore del coefficiente di correlazione tra le variabili, dipendente e indipendente, e il coefficiente angolare della retta di regressione.
es 20.
Esempio di applicazione della regressione lineare a dati fMRI.
Per una brevissima introduzione alla tecnica fMRI vedere qui.
La variabile indipendente la descrizione del paradigma sperimentale: consiste in una serie di 0 e 1. Il valore '0' indica 'nessun compito svolto da parte del soggetto', il valore '1' indica 'svolgimento del compito da parte del soggetto'.
La variabile dipendente il segnale ottenuto tramite risonanza magnetica per immagini (MRI), dove si utilizzato l'effetto BOLD (Blood Oxygenation Level Dependent). é stato acquisito il segnale in corrispondenza degli stati sopradescritti ('0' e '1').
Si chiede di considerare tre casi, corrispondenti a misure effettuate in diverse regioni cerebrali.
Le variabili sono contenute in tre file differenti (serie_37_36.mat, serie_37_37.mat, serie_42_30.mat). La variabile indipendente contenuta nel file paradigma_2.mat.
Per ogni caso considerato, fare il grafico della distribuzione delle misure, della retta di regressione.
Calcolare l'errore del modello di regressione in corrispondenza di ogni valore della variabile indipendente e farne l'istogramma.